fantasticnax.blogg.se - Volume occupied by atoms hcp

The orbitals in the solid are constructed in the same way as those in a molecule, but they apply to a crystal rather than a molecule, so they are called crystal orbitals rather than molecular orbitals. The explanation, which is called band theory, applies the concepts presented in the molecular orbital discussion in Chapter 6 to a very large number of orbitals. Introduction to Band Theory The molecular orbital description of the delocalized electrons in metallic bonds provides a more complete picture of metallic bonding as well as an explanation for the electrical conductivity of metals.

Distinguish between a metallic conductor, a semiconductor, and an insulator based on their band structures.Ĩ.6-1.

The tighter packing of γ-iron makes it so corrosion-resistant that it is known as stainless steel. Iron normally crystallizes with a bcc structure known as α-iron, but it also can be made to adopt a more efficiently packed fcc structureĬalled γ-iron by adding small amounts of carbon and manganese or nickel and chromium. The effect can also be seen by comparing two forms of iron. Ca isĪlmost 60% more dense because it crystallizes in the more efficient fcc unit cell. The impact of packing efficiency on the density can be seen by comparing K and Ca, which are next to one another in the periodic chart and have nearly identical metallic radii. The densities of the Group 1A elements are all quite low because their atoms are not very dense (they have the greatest volume and smallest mass of any atom in their period) and because they pack in the less efficient bcc lattice. Indeed, the only known example of a metal adopting the sc unit cell is a form of polonium. Almost half of the volume of a sc unit cell is void space, so the sc unit cell is not a favorable way to pack and metals do not generally crystallize in sc lattices. Packing Efficiency and Crystal Properties Table 8.3 shows the unit cell types, metallic radii, and densities of selected metals that adopt cubic unit cells. Table 8.2: Packing Efficiencies and Coordination Numbers of Cubic Lattices 8.5-7. A three-dimensional lattice is formed by translation of a three-dimensional unit cell in three directions. Continued operations of translation generate the complete crystalline lattice. Translation by the length of one of the cell edges of either cell in any of the four directions produces an adjacent cell. One unit cell consists of four A's on the corners and a B in the face center, while the other has B's on the corners with an A in the center. The figure shows two different but equivalent unit cells in a two-dimensional array.

When the unit cell is repeated in all three directions, it generates the entire crystalline lattice. The simplest portion of the lattice that makes up the repeating unit is called the unit cell. The pattern of the array is called the crystal lattice, and the individual positions are called lattice sites. Crystalline solids are orderly, repeating, 3-D arrays of particles, which can be atoms, ions, or groups of atoms, such as polyatomic ions or molecules. The unit cell is the smallest repeat unit of the crystalline lattice that generates the entire lattice with translation. In this section, we define the unit cell and discuss how it is packed with atoms. Our study is simplified because, instead of studying the positions of the enormous number of particles that constitute the entire crystal, we need study only the small number of particles that comprise a unit cell. 8.1 Unit Cells Introduction However, the long range order that characterizes crystalline solids means that there is a small repeat unit, called the unit cell, that can be used to generate the entire crystal.

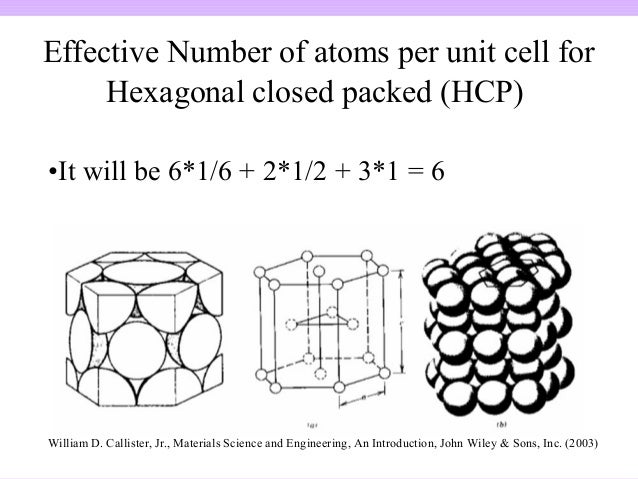
Thus, studying the solid state could be a formidable task. Even a small crystal contains millions and millions of particles. This chapter is devoted to the study of crystalline solids. Table salt and sugar are two common examples of crystalline solids.

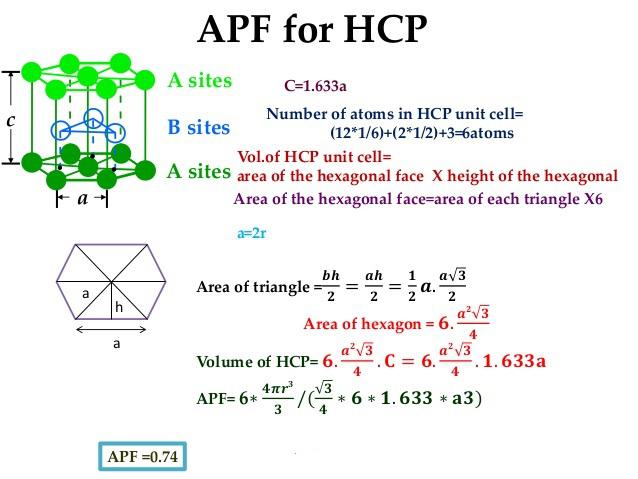
If the order exists throughout the entire solid (long range order), the solid is said to be a crystalline solid. If the order is over short distances only (local order), the solid is an amorphous solid. Therefore, the atomic packing fraction for HCP is equal to the 0.74.Chapter 8 – Solids Introduction Solids are characterized by an orderly arrangement of their particles. For the hexagonal close packing structure$(\text=0.74\] Hint: The volume of the unit cell can be determined by taking the product of the area and height of the cell.